---
title: "Insurance Cost Forecast by using Linear Regression"
author: "Rafiq Islam"
date: 2024-09-12
search: true
---
# Data Gathering, Defining Stakeholders and KPIs
## Data Loading
```{python}
#| code-fold: false
import pandas as pd
insurance = pd.read_csv('insurance.csv')
insurance.sample(5, random_state=111)
```
## Exploratory Data Analysis (EDA)
### Data Information
```{python}
#| code-fold: false
insurance.info()
```
No missing data. Total 1338 observations.
### Data Description
Statistical properties of the non-categorical variables
```{python}
#| code-fold: false
print(insurance.describe())
```
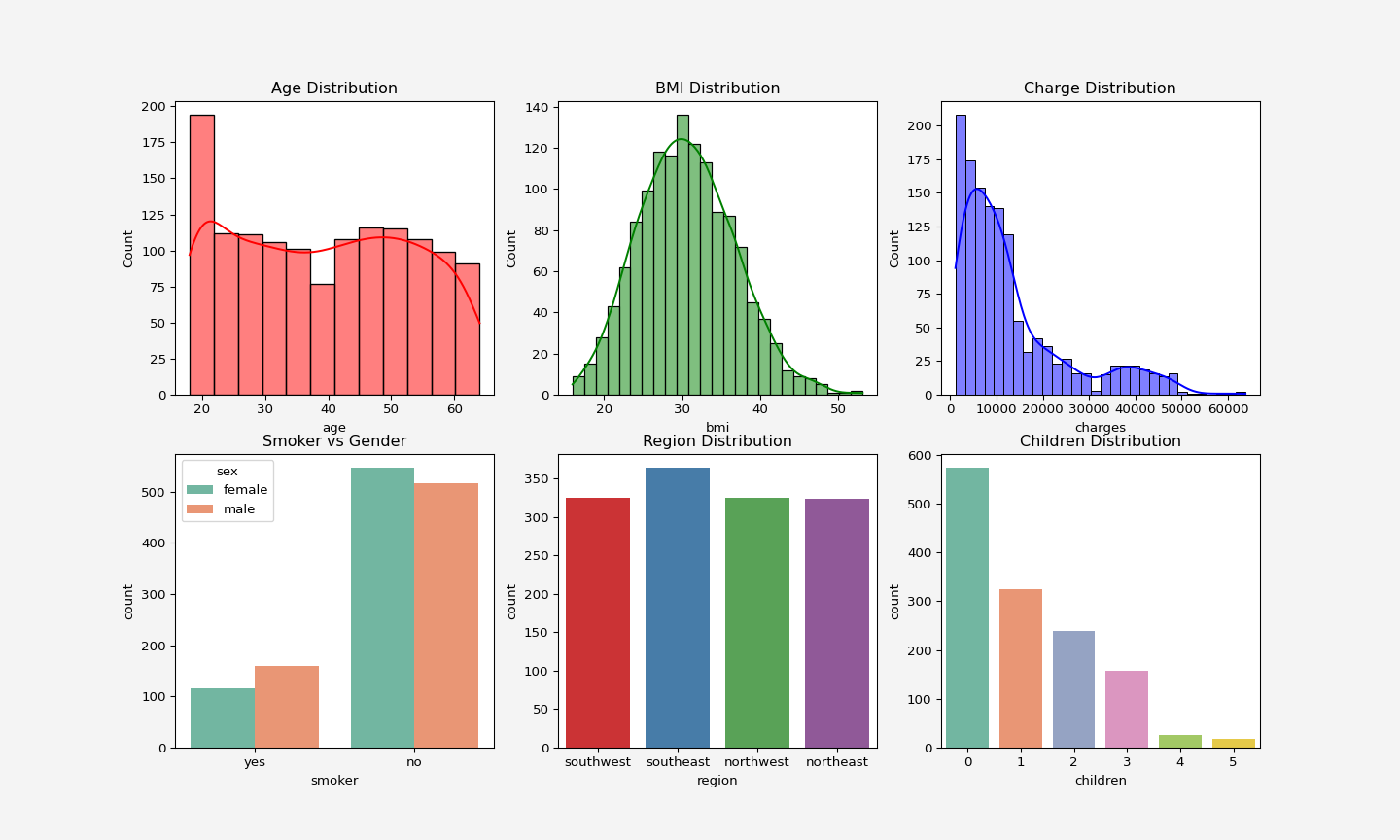
### Data visualization
#### Distribution of the features and target
```{python}
#| code-fold: false
#| output: false
import seaborn as sns
import matplotlib.pyplot as plt
fig, axes = plt.subplots(2,3,figsize = (15,9))
sns.histplot(insurance['age'], color='red', kde=True, ax= axes[0, 0]).set_title('Age Distribution')
sns.histplot(insurance['bmi'], color='green', kde=True, ax= axes[0,1]).set_title('BMI Distribution')
sns.histplot(insurance['charges'],color='blue', kde=True, ax= axes[0,2]).set_title('Charge Distribution')
sns.countplot(x='smoker', data=insurance, hue='sex', palette='Set2', ax=axes[1,0]).set_title('Smoker vs Gender')
sns.countplot(x=insurance['region'], hue=insurance['region'], palette='Set1', ax=axes[1,1]).set_title('Region Distribution')
sns.countplot(x=insurance['children'], hue=insurance['children'],legend=False,palette='Set2', ax=axes[1,2]).set_title('Children Distribution')
plt.gcf().patch.set_facecolor('#f4f4f4')
```
<p align="center">
<img src="dataviz.png" alt="Data Vizualization" width="900" height="550"/>
</p>
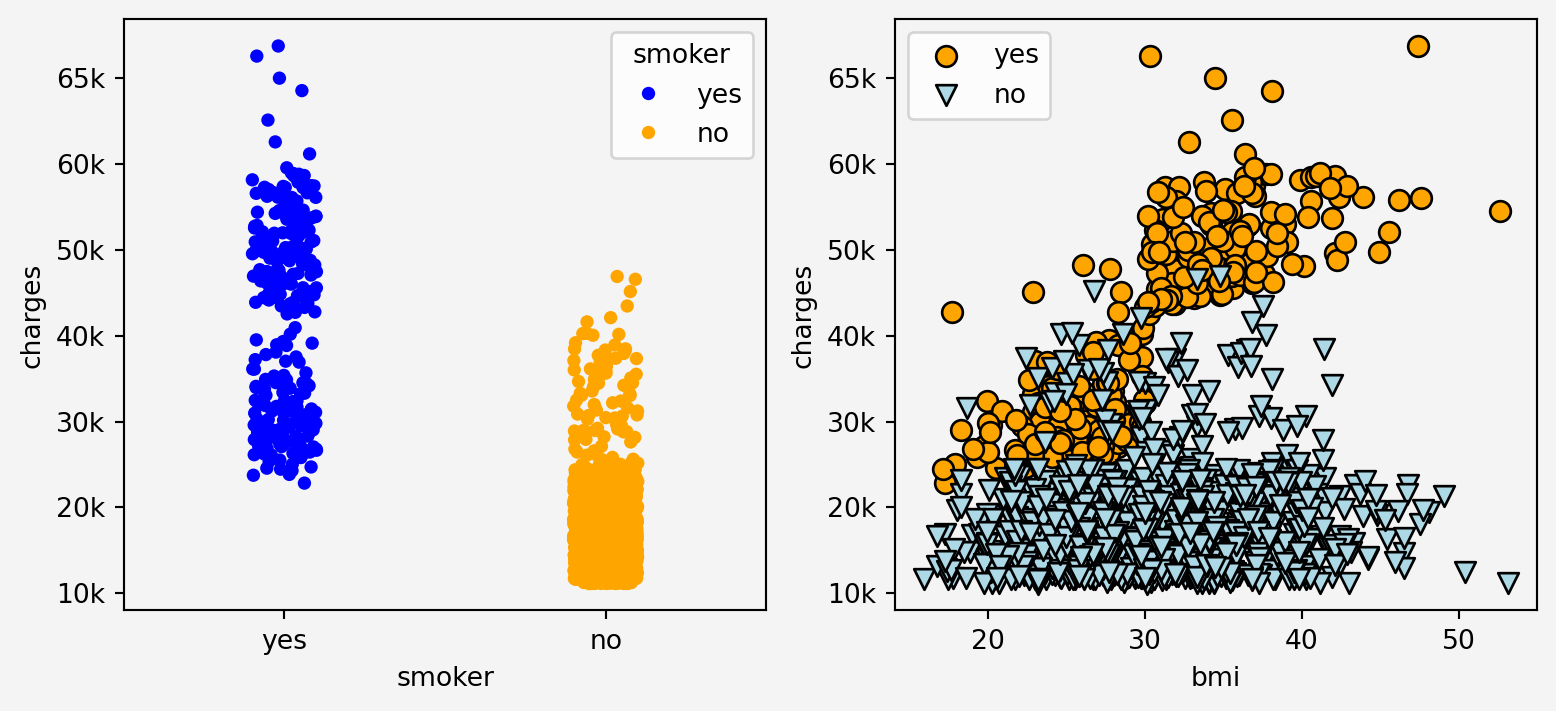
#### Relationship of the features and target
```{python}
#| code-fold: false
#| warning: false
fig, axes = plt.subplots(1,2, figsize=(9.5,4))
g=sns.stripplot(data=insurance, x='smoker', y='charges', hue='smoker' ,palette=['blue', 'orange'], legend=True, ax=axes[0])
g.set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
axes[1].scatter(insurance.loc[insurance.smoker=='yes'].bmi,
insurance.loc[insurance.smoker=='yes'].charges, label="yes", marker='o',
s=60,edgecolors='black', c='orange'
)
axes[1].set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
axes[1].scatter(insurance.loc[insurance.smoker=='no'].bmi,
insurance.loc[insurance.smoker=='no'].charges, label="no", marker='v',
s=60,edgecolors='black', c='lightblue'
)
axes[1].set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
axes[1].set_xlabel('bmi')
axes[1].set_ylabel('charges')
axes[1].legend()
for ax in axes:
ax.set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
Clearly from the plots above we can see that the somoking status has effect on the insurance charges in relation with bmi
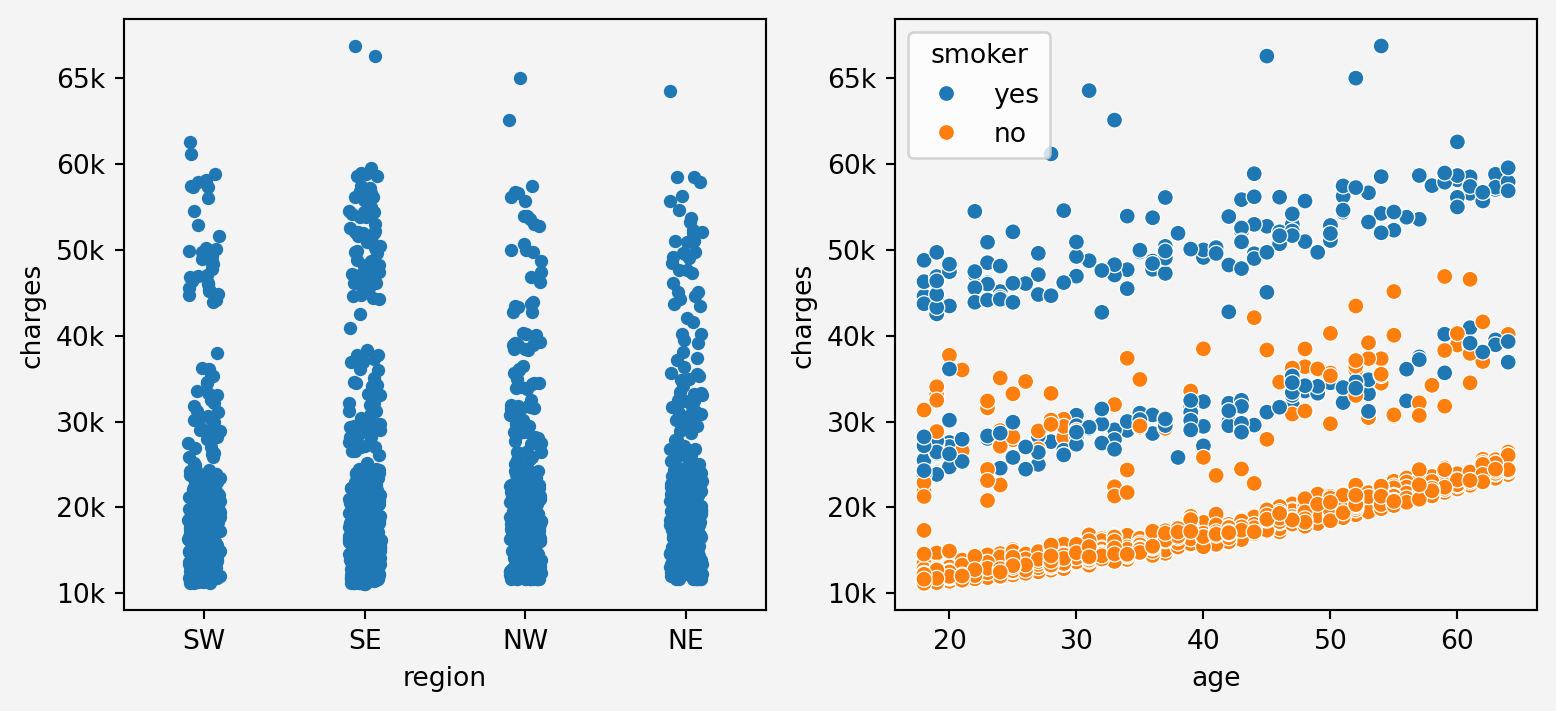
```{python}
#| code-fold: false
#| warning: false
fig, axes = plt.subplots(1,2,figsize=(9.5,4))
g1=sns.stripplot(x='region', y='charges', data=insurance, ax=axes[0])
g1.set_xticklabels(['SW', 'SE', 'NW','NE'])
g1.set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
g2=sns.scatterplot(x='age', y='charges', data=insurance, hue='smoker' ,ax=axes[1])
g2.set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
for ax in axes:
ax.set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
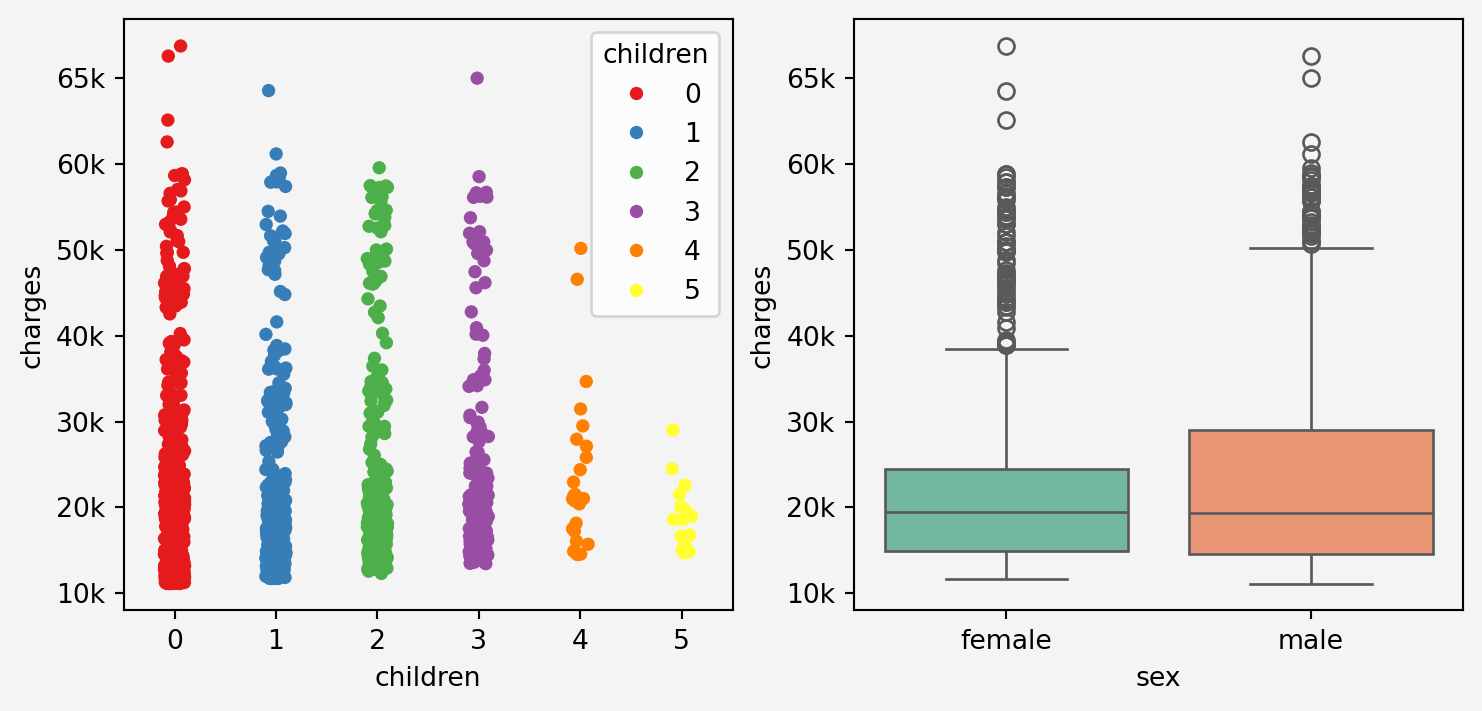
```{python}
#| code-fold: false
#| warning: false
fig, axes = plt.subplots(1,2, figsize=(9,4))
g1=sns.stripplot(x='children', y='charges',data=insurance,hue='children',palette='Set1', ax=axes[0])
g1.set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
g1.set_facecolor('#f4f4f4')
g2=sns.boxplot(x='sex', y='charges', data=insurance, hue='sex', palette='Set2', ax=axes[1])
g2.set_yticklabels(['0k','10k','20k','30k','40k','50k','60k','65k'])
g2.set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
To see the combined effect of all the features
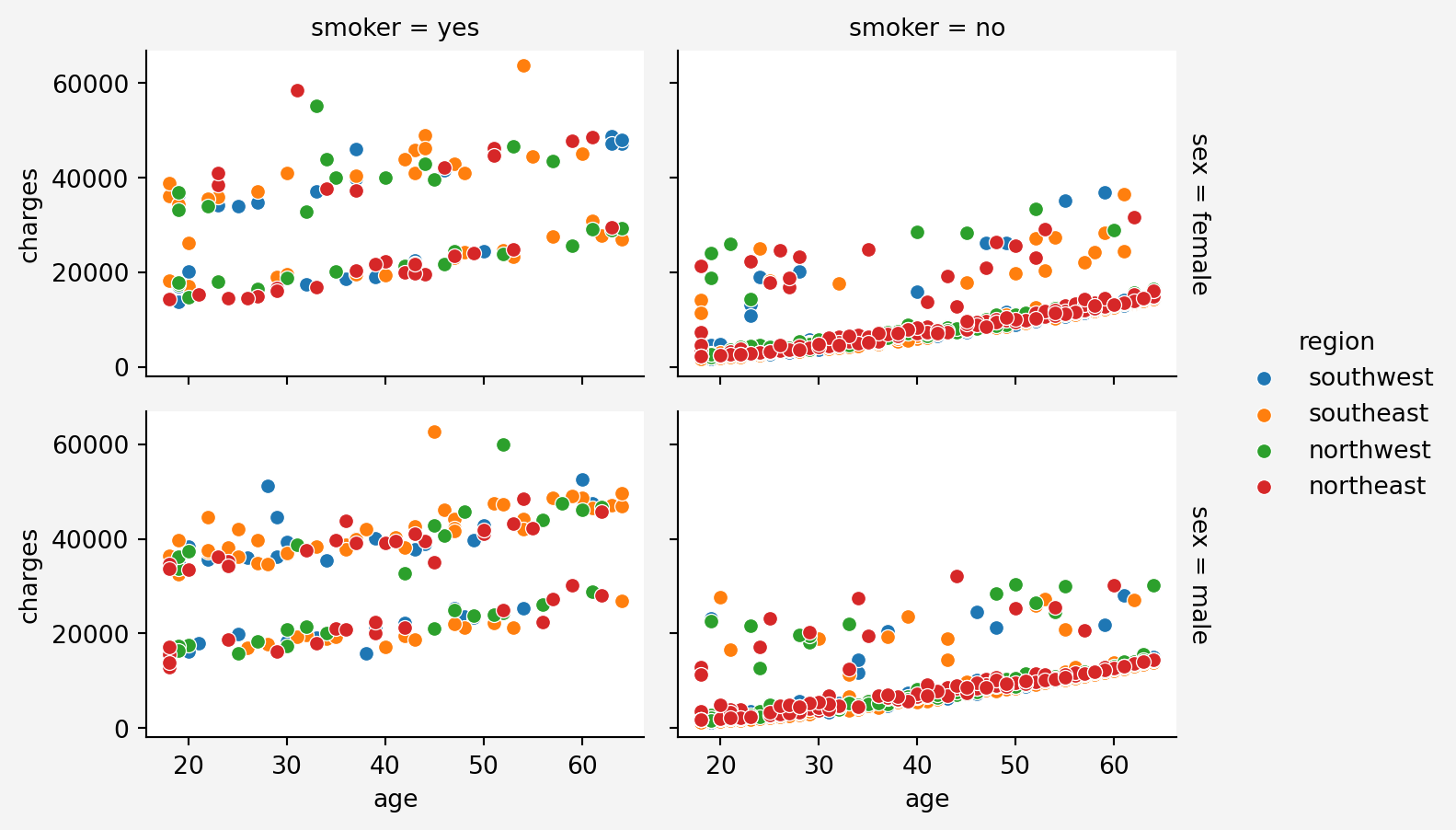
```{python}
#| code-fold: false
#| warning: false
plt.figure(figsize=(12,6))
g = sns.FacetGrid(insurance, col='smoker', row='sex',hue='region', margin_titles=True, height=2.4, aspect=1.5)
g.map(sns.scatterplot, 'age','charges')
g.fig.patch.set_facecolor('#f4f4f4')
g.add_legend()
plt.show()
```
#### Information Gain
From the above plots, we can see that `age` feature stacks in three layers for charges. It maybe depending on other categorical features such as smoking status.
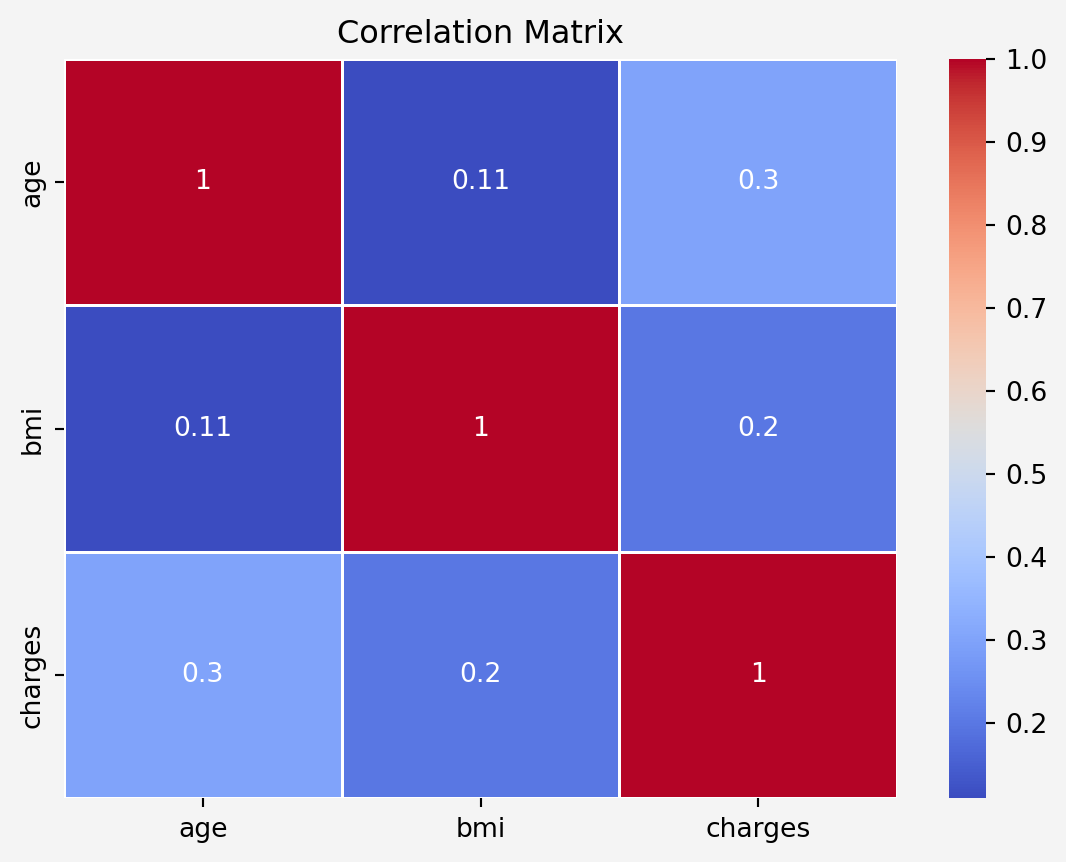
### Correlation Analysis
#### Contineous Features
```{python}
#| code-fold: false
corr_matrix = insurance[['age','bmi','charges']].corr()
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title('Correlation Matrix')
plt.gca().set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
#### Categorical Features
```{python}
#| code-fold: false
import scipy.stats as st
anova_sex, p_value1 = st.f_oneway(
insurance[insurance['sex']=='male']['charges'],
insurance[insurance['sex']=='female']['charges']
)
anova_smoker, p_value2 = st.f_oneway(
insurance[insurance['smoker']=='yes']['charges'],
insurance[insurance['smoker']=='no']['charges']
)
anova_region, p_value3 = st.f_oneway(
insurance[insurance['region']=='southwest']['charges'],
insurance[insurance['region']=='southeast']['charges'],
insurance[insurance['region']=='northwest']['charges'],
insurance[insurance['region']=='northeast']['charges']
)
anova_children, p_value4 = st.f_oneway(
insurance[insurance['children']==0]['charges'],
insurance[insurance['children']==1]['charges'],
insurance[insurance['children']==2]['charges'],
insurance[insurance['children']==3]['charges'],
insurance[insurance['children']==4]['charges'],
insurance[insurance['children']==5]['charges']
)
anova_results = {
'feature_name': ['sex', 'smoker', 'region', 'children'],
'F-Statistic':[anova_sex, anova_smoker,anova_region,anova_children],
'p-value':[p_value1, p_value2, p_value3, p_value4]
}
anova = pd.DataFrame(anova_results)
print(anova)
```
#### Information Gain
Both `age` and `bmi` features are positively correlated to `charges` with correlation coefficients $0.3$ and $0.2$, respectively. Since the $p$-values are less thatn $0.05$, therefore, all the categorical features have impact on the target features.
## Pre-processing
### Data Cleaning
```{python}
#| code-fold: false
# Binary Encoding for the variables with two categories
from sklearn.preprocessing import LabelEncoder
insurance['male'] = pd.get_dummies(insurance.sex, dtype=int)['male']
insurance['smoke'] = pd.get_dummies(insurance.smoker, dtype=int)['yes']
insurance.drop(['sex','smoker'],axis=1, inplace=True)
label_encoder = LabelEncoder()
insurance['region']=label_encoder.fit_transform(insurance['region'])
new_order = ['age', 'bmi', 'male', 'smoke','children','region', 'charges']
insurance = insurance[new_order]
insurance['charges'] = insurance['charges'].round(2)
insurance.sample(5)
```
### Check for Multicollinearity
```{python}
#| code-fold: false
from statsmodels.stats.outliers_influence import variance_inflation_factor
X = insurance.drop('charges', axis=1)
vif_data = pd.DataFrame()
vif_data['feature'] = X.columns
vif_data['VIF'] = [variance_inflation_factor(X.values,i) for i in range(len(X.columns))]
print(vif_data)
```
Since BMI and Age have higher values for the multicolinearity, therefore we adopt the following methods
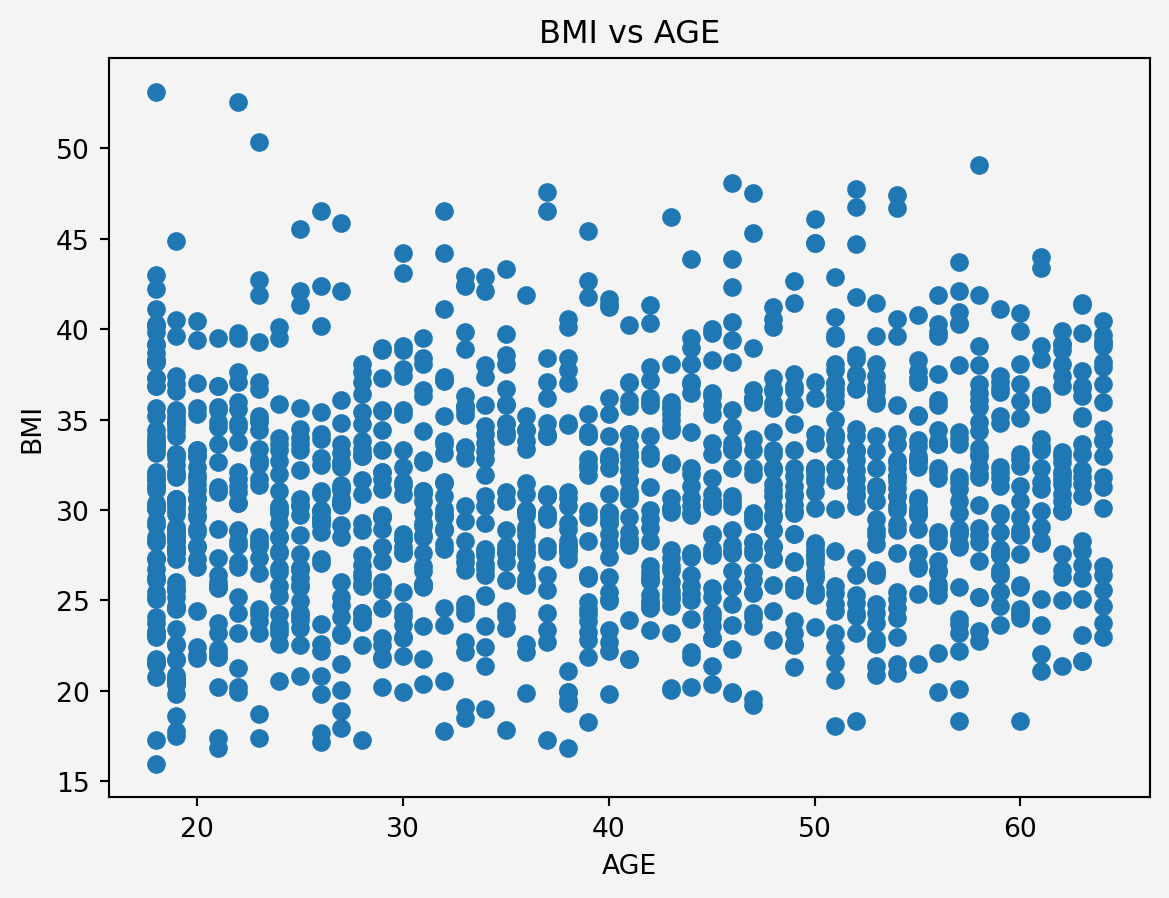
### Feature Engineering
#### Interaction term
```{python}
#| code-fold: false
plt.scatter(insurance.age,insurance.bmi)
plt.xlabel('AGE')
plt.ylabel('BMI')
plt.title('BMI vs AGE')
plt.gca().set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
<p style="text-align: justify">
Since there is no clear linear relationship or any pattern, the Multicollinearity issue can be ignored. However, older individuals with a certain BMI range might have different risks or costs associated with their health. We could explore interaction terms like `age` * `bmi` in our model to capture any potential synergistic effects.
</p>
```{python}
#| code-fold: false
insurance.insert(6,'age_bmi',insurance.age*insurance.bmi)
insurance.insert(7,'age_bmi_smoke',insurance.age_bmi*insurance.smoke)
insurance.sample(5,random_state=111)
```
### Data Splitting
```{python}
#| code-fold: false
from sklearn.model_selection import train_test_split
X = insurance.drop('charges',axis=1)
y = insurance['charges'].to_frame()
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.30, random_state=42)
```
### Standardization
```{python}
#| code-fold: false
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
conts_features = ['age','bmi','age_bmi']
categ_features = ['male','smoke', 'children','region']
preprocessor = ColumnTransformer(
transformers=[
('num', StandardScaler(), conts_features)
],
remainder= 'passthrough'
)
X_train_sc = preprocessor.fit_transform(X_train)
X_test_sc = preprocessor.fit(X_test)
```
# Model
## Modelling Approaches
We consider the following models
1. **Baseline model:** Assumption that the `charges` variable can be modeled with the mean value of this `charges` variable.
$$
\text{charges}=\mathbb{E}[\text{charges}]+\xi
$$
2. **Linear Regression with `age-bmi-smoke` interaction**
$$
\text{charges}=\beta_0+\beta_1 (\text{age\_bmi})+\beta_2 (\text{male})+\beta_3 (\text{smoke})+\beta_4 (\text{children})+\beta_5 (\text{region})+\beta_6 (\text{age-bmi-smoke})+\xi
$$
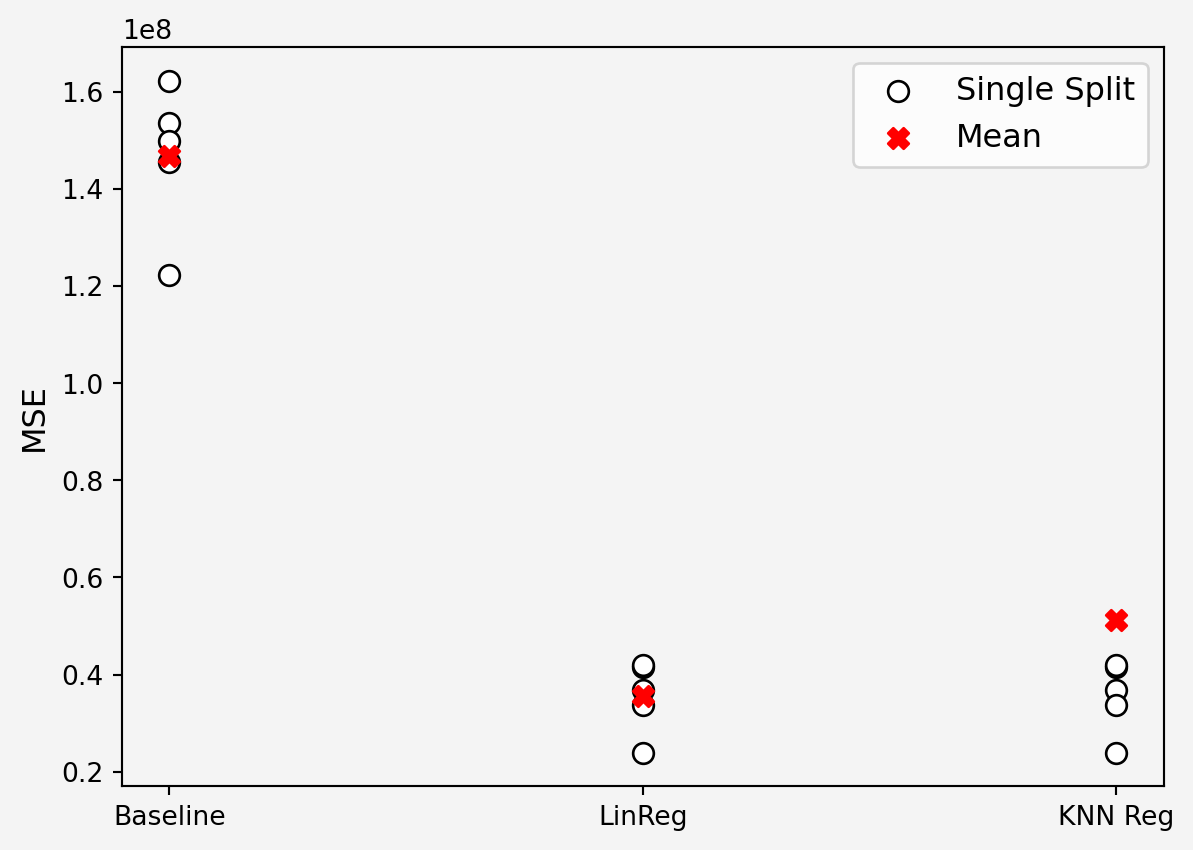
3. **K-Neighbor Regression**
$k$NN using all the original feature
```{python}
#| code-fold: false
import numpy as np
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
kfold = KFold(n_splits=5,shuffle=True, random_state=111)
mses = np.zeros((3,5))
k = 10
for i, (train_index, test_index) in enumerate(kfold.split(X_train_sc)):
X_train_sc_train = X_train_sc[train_index]
X_train_sc_holdout = X_train_sc[test_index]
y_train_train = y_train.iloc[train_index]
y_train_holdout = y_train.iloc[test_index]
pred0 = y_train_train.charges.mean()*np.ones(len(test_index))
model1 = LinearRegression()
model2 = KNeighborsRegressor(k)
model1.fit(X_train_sc_train[:,2:], y_train_train)
model2.fit(X_train_sc_train[:,:6], y_train_train)
pred1 = model1.predict(X_train_sc_holdout[:,2:])
pred2 = model2.predict(X_train_sc_holdout[:,:6])
mses[0,i] = mean_squared_error(y_train_holdout, pred0)
mses[1,i] = mean_squared_error(y_train_holdout, pred1)
mses[2,i] = mean_squared_error(y_train_holdout, pred2)
plt.scatter(np.zeros(5), mses[0,:],s=60, c='white', edgecolors='black', label='Single Split')
plt.scatter(np.ones(5), mses[1,:], s=60, c='white', edgecolors='black')
plt.scatter(2*np.ones(5), mses[1,:], s=60, c='white', edgecolors='black')
plt.scatter([0,1,2],np.mean(mses, axis=1),s=60, c='r', marker='X', label='Mean')
plt.legend(loc='upper right', fontsize=12)
plt.xticks([0,1,2],['Baseline','LinReg','KNN Reg'])
plt.yticks(fontsize=10)
plt.ylabel('MSE',fontsize=12)
plt.gca().set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
```{python}
#| code-fold: false
print(np.mean(np.sqrt(mses),axis=1))
print('\n')
print('Minimum RMSE={} \n Model {}'.format(min(np.mean(np.sqrt(mses),axis=1)),np.argmin(np.mean(np.sqrt(mses),axis=1))) )
```
## Final Model
```{python}
#| code-fold: false
#| warning: false
from sklearn.pipeline import Pipeline
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.preprocessing import OneHotEncoder
data = pd.read_csv('insurance.csv')
class FeatureEngineering(BaseEstimator, TransformerMixin):
def __init__(self):
# Initialize OneHotEncoder for 'smoker' and 'sex'
self.ohe_smoker_sex = OneHotEncoder(
drop='first', dtype=int, sparse_output=False)
self.label_encoder = LabelEncoder()
def fit(self, X, y=None):
# Fit the OneHotEncoder on smoker and sex
self.ohe_smoker_sex.fit(X[['smoker', 'sex']])
self.label_encoder.fit(X['region'])
return self
def transform(self, X):
X = X.copy()
# Apply OneHotEncoder to 'smoker' and 'sex'
smoker_sex_encoded = self.ohe_smoker_sex.transform(
X[['smoker', 'sex']])
smoker_sex_columns = ['smoker_yes', 'sex_male']
# Create DataFrame for encoded variables and merge with original data
smoker_sex_df = pd.DataFrame(
smoker_sex_encoded, columns=smoker_sex_columns, index=X.index)
X = pd.concat([X, smoker_sex_df], axis=1)
# Label encode the 'region' column
X['region'] = self.label_encoder.transform(X['region'])
# Create new features
X['age_bmi'] = X['age'] * X['bmi']
X['age_bmi_smoker'] = X['age_bmi'] * X['smoker_yes']
# Drop original columns
X = X.drop(columns=['age', 'bmi', 'smoker', 'sex'])
return X
data = pd.read_csv('insurance.csv')
data['charges'] = data['charges'].round(2)
X = data.drop('charges', axis=1)
y = data['charges']
preprocessor = ColumnTransformer(
transformers=[
('scale', StandardScaler(), ['age_bmi', 'age_bmi_smoker'])
],
remainder='passthrough'
)
pipe = Pipeline(steps=[
('feature_engineering', FeatureEngineering()),
('preprocess', preprocessor),
('model', LinearRegression())
])
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, shuffle=True, random_state=111
)
pipe.fit(X_train, y_train)
print(np.round(pipe['model'].intercept_,2))
```
## Model Validation
### Root Mean Squared Error (RMSE)
```{python}
#| code-fold: false
train_prediction = pipe.predict(X_train)
test_prediction = pipe.predict(X_test)
print("Training set RMSE:",
np.round(np.sqrt(mean_squared_error(train_prediction,y_train)))
)
print("Test set RMSE:",
np.round(np.sqrt(mean_squared_error(test_prediction,y_test)))
)
```
### R-Squared ($R^2$)
```{python}
#| code-fold: false
from sklearn.metrics import r2_score
y_pred = pipe.predict(X_test)
r2 = r2_score(y_test, y_pred)
print(f'R-squared: {r2:.4f}')
```
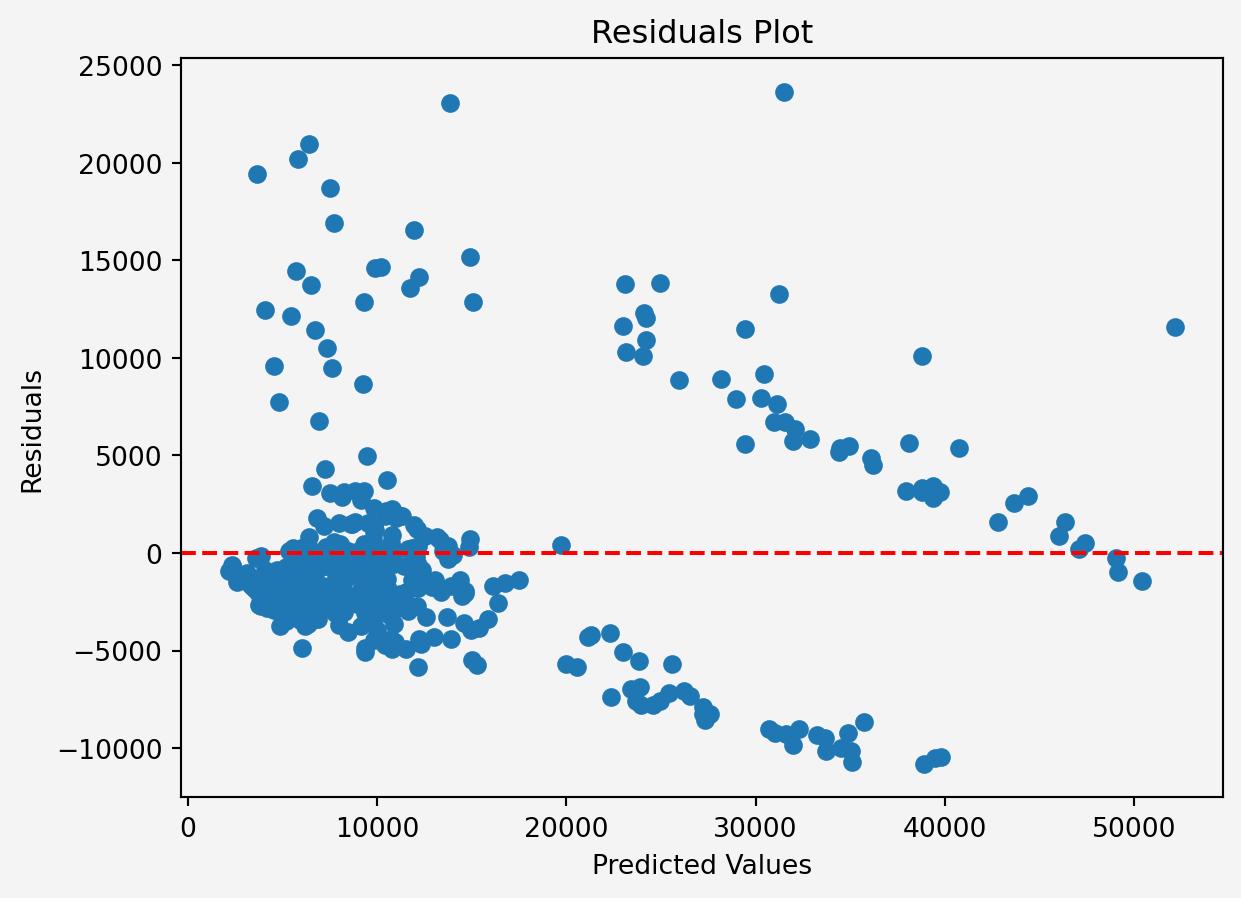
### Residuals
```{python}
#| code-fold: false
res = y_test - y_pred
plt.scatter(y_pred, res)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.title('Residuals Plot')
plt.gca().set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
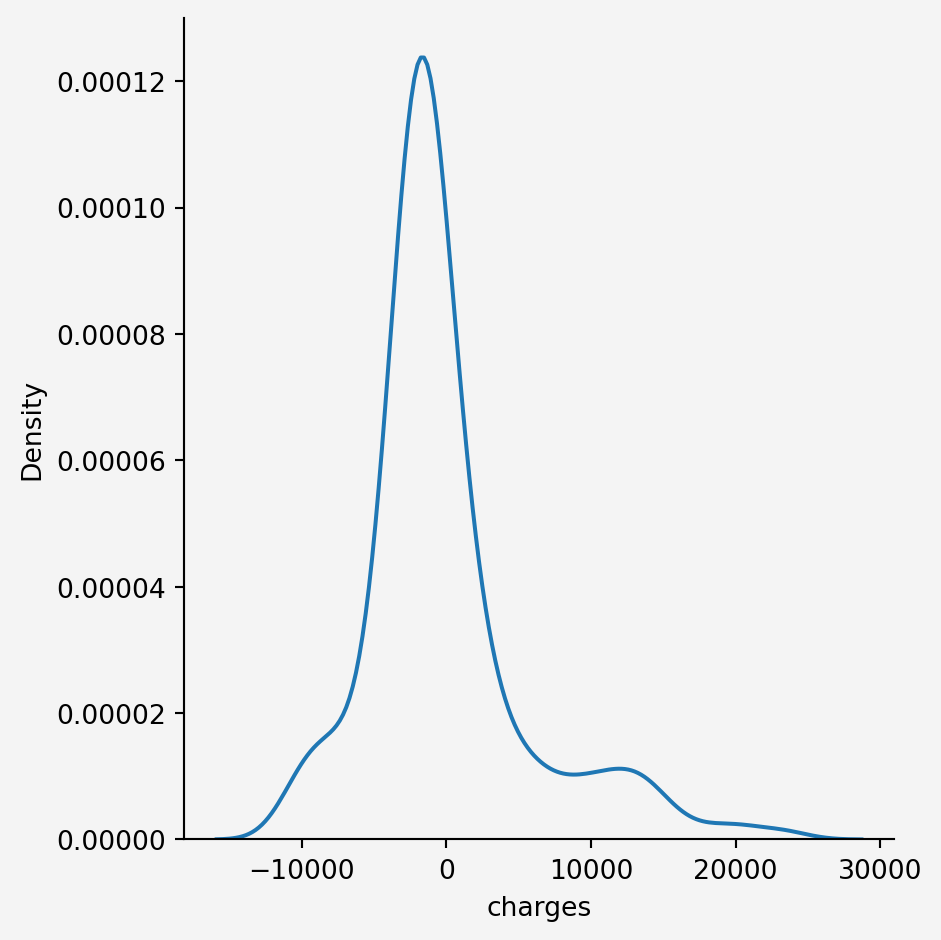
```{python}
#| code-fold: false
sns.displot(res,kind='kde')
plt.gca().set_facecolor('#f4f4f4')
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()
```
# Development and Deployment
```{python}
#| code-fold: false
import pickle
pickle.dump(pipe, open('regmodel.pkl','wb'))
```