Matrix decomposition: Understanding Eigendecomposition - A Fundamental Tool in Linear Algebra

In many areas of data science, machine learning, and applied mathematics, eigendecomposition is a core technique for understanding and transforming data. Whether you’re working with dimensionality reduction (like PCA), solving systems of differential equations, or analyzing graph structures, chances are you’ll run into eigenvalues and eigenvectors.

---

What Is Eigendecomposition?

Eigendecomposition is a way of breaking down a square matrix into a set of simpler components based on its eigenvalues and eigenvectors.

For a given square matrix \(A\), if we can find a basis of eigenvectors, then \(A\) can be expressed as:

\[ A = Q \Lambda Q^{-1} \]

Where:

• \(Q\) is a matrix whose columns are the eigenvectors of \(A\).
• \(\Lambda\) (capital lambda) is a diagonal matrix containing the eigenvalues of \(A\) along its diagonal.
• \(Q^{-1}\) is the inverse of \(Q\).

This is essentially rewriting \(A\) as a combination of scaling operations along special directions (the eigenvectors).

Eigenvalues and Eigenvectors Recap

Before decomposition, we need to understand the building blocks:

Given a square matrix \(A\), an eigenvector \(\mathbf{v}\) and eigenvalue \(\lambda\) satisfy:

\[ A \mathbf{v} = \lambda \mathbf{v} \]

• \(\mathbf{v}\) is a direction in which the transformation \(A\) acts by stretching or compressing without rotating it.
• \(\lambda\) tells us how much \(A\) scales \(\mathbf{v}\).

Example: If \(A \mathbf{v} = 3 \mathbf{v}\), then \(\mathbf{v}\) is scaled by a factor of 3 under \(A\).

When Can We Use Eigendecomposition?

Not all matrices can be decomposed this way.

• Eigendecomposition is possible for diagonalizable matrices, i.e., matrices with enough linearly independent eigenvectors to form a basis.
• Symmetric matrices (in real-valued cases) are always diagonalizable and have orthogonal eigenvectors.

If a matrix is defective (doesn’t have enough eigenvectors), we can’t use eigendecomposition directly — but other decompositions (like Jordan decomposition or SVD) still work.

Why Is This Useful?

Eigendecomposition lets us simplify matrix operations by working in a new coordinate system defined by eigenvectors.

If:

\[ A = Q \Lambda Q^{-1} \]

Then:

\[ A^k = Q \Lambda^k Q^{-1} \]

Where \(\Lambda^k\) is just the diagonal matrix with each eigenvalue raised to the \(k\)-th power. This makes repeated multiplications or exponentials of matrices much easier.

Applications in Data Science and Beyond

Principal Component Analysis (PCA)

• PCA uses eigendecomposition of the covariance matrix to find the principal directions of data variability.
• Eigenvectors correspond to directions of maximum variance; eigenvalues tell you how much variance is captured.

Solving Systems of Differential Equations

• Linear ODE systems can be solved by diagonalizing the system matrix.

Graph Analysis

• In spectral graph theory, eigenvalues of adjacency or Laplacian matrices reveal connectivity and clustering properties.

Markov Chains

• The steady state of a Markov process is related to the eigenvector corresponding to eigenvalue \(\lambda = 1\).

---

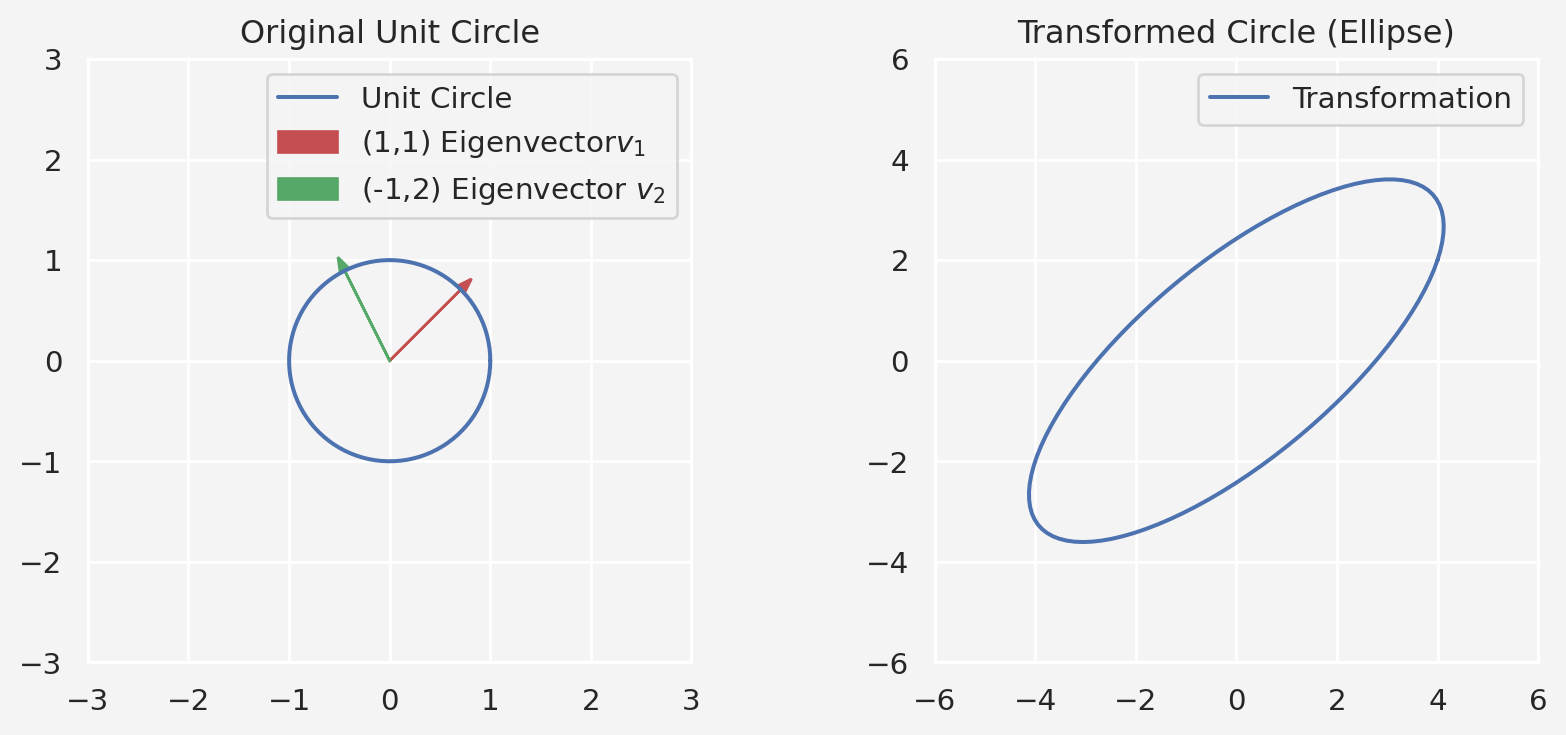
A Simple Example

Let’s take:

\[ A = \begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \]

1. Find eigenvalues by solving:

\[ \det(A - \lambda I) = 0 \]

\[ (4 - \lambda)(3 - \lambda) - 2 = \lambda^2 - 7\lambda + 10 = 0 \]

\[ \lambda_1 = 5, \quad \lambda_2 = 2 \]

2. Find eigenvectors by solving \((A - \lambda I)\mathbf{v} = 0\).

• For \(\lambda = 5\): eigenvector \(\mathbf{v}_1 = [1, 1]^T\)
• For \(\lambda = 2\): eigenvector \(\mathbf{v}_2 = [-1, 2]^T\)

3. Form Q and \(\Lambda\):

\[ Q = \begin{bmatrix} 1 & -1 \\ 1 & 2 \end{bmatrix}, \quad \Lambda = \begin{bmatrix} 5 & 0 \\ 0 & 2 \end{bmatrix} \]

4. Check:

\[ A = Q \Lambda Q^{-1} \]

---

Visualization.

Key Takeaways

• Eigendecomposition = diagonalization of a matrix via eigenvalues and eigenvectors.
• Only works for diagonalizable matrices, but symmetric matrices are guaranteed to work.
• Simplifies many computations, from raising matrices to powers to solving ODEs.
• Foundation for PCA, spectral graph analysis, and many machine learning methods.

---

Tip: If your matrix isn’t diagonalizable, try Singular Value Decomposition (SVD) — it works for any matrix and generalizes many of the benefits of eigendecomposition.

Share on

You may also like